Fun With Linear Time: My Favorite Algorithm

Boyer–Moore majority vote algorithm — I love this algorithm because it's amazing and approachable. I first saw it on a LeetCode discuss thread, and it blew everyone away. Some people were, like, irate. (169) Majority Element.

This problem, common on competitive coding sites, has a solution that was discovered in 1980 but went unpublished until 1991 because of its emphasis on Fortran and mechanical verification.

Problem: Given a list of votes with a majority (n/2 + 1), declare the leader. As in, the most frequently occurring vote. It is possible to get the result in linear time O(n) AND constant space O(1).

Examples:

[0, 1, 1, 0, 1, 0, 1, 1] => 1 is the majority element

['a', 'b', 'a', 'c', 'b', 'c', 'a', 'a'] => 'a' is the majority here

A naive solution might look like this. We'll use a Dictionary to keep track of all the votes as well as storing the highest number of votes we've seen.

def majority_vote(votes):
    leader = None
    max_votes = 0
    candidates = dict()

    for i in votes:
        # if seen before
        if i in candidates:
            # count their vote
            candidates[i] += 1
            # and check if they're leading
            if candidates[i] > max_votes:
                leader = i
                max_votes = candidates[i]
        else:
            candidates[i] = 1

    return leader

The above accomplishes a correct solution in linear time O(n) using linear space O(n). We can do better. One pass, without counting every element.

MJRTY or A Fast Majority Vote Algorithm was discovered in the Computer Science Laboratory of SRI International in 1980 by Robert S. Boyer and J Strother Moore. They were assisting a colleague who was working on fault tolerance.

In their humorous paper, they imagined a convention center filled with voters, carrying placards boasting the name of their chosen candidate. Each voter representing an index of the list.

Suppose a floor fight ensues

They opined that the voters might knock each other out simultaneously, going only for the opposing team. After the mess, the voter/s left standing would represent the majority.

Here is a bloodless way the chairman can simulate the pairing phase.

Their algorithm improves on our naive solution by removing the data structure (the Dictionary). Converted here from Fortran to Python.

def majority_vote_improved(votes):
    # after one vote, we have a leader
    leader = votes[0]
    count = 1

    for i in range(1, len(votes)):
        # the lead may grow
        if votes[i] == leader:
            count += 1
        else:
            # or shrink
            count -= 1

        # and they may be replaced
        if count == 0:
            leader = votes[i]
            count = 1

    return leader

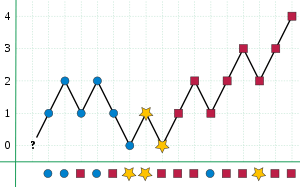
Thus, the majority is found in linear time O(n) with constant space O(1).

Check out a step-by-step walkthrough on Moore's website. More on Wikipedia too.

The entire effort of specifying MJRTY and getting the 61 verification conditions proved required about 20 man hours. [...] about 55 minutes of computer time to prove the final list of 66 theorems.