There are many parallels between chess engines and Sokoban solvers. Both games have a large branching factor, and similar algorithms and techniques are shared between them. However, unlike the game of chess where computers reign supreme, complex Sokoban puzzles are out of reach for automated solvers.

I set out to build a Sokoban game, and a naïve solver, to explore this space.
Building
Sokoban puzzles are shared in plain text files using a community-defined level format.
wall: #player: @player on goal: +box: $box on goal: *goal: .floor: (space)
Levels are surrounded by walls and have an equal number of boxes and goals. Here's a small level that can be solved in three key presses. The player @ needs to travel two positions right, and then push the box $ onto the goal.
########@ $.########
Solutions have a community-defined format too; a list of concatenated directions — lowercase for moves and uppercase for pushes. l for left, r for right, etc.
The above level has a solution of rrR (two moves right, and then a push right). We can track if the level is complete by checking that there are zero box characters $ (they should all be the box-on-goal character *).
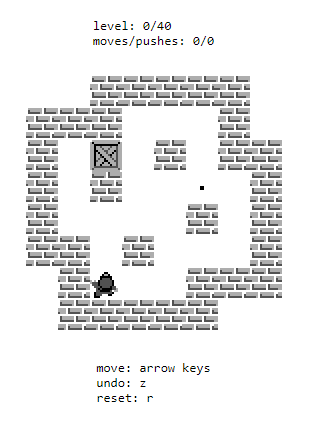
My Sokoban game stores level state in a 2D array. It's not the most efficient representation but it's easier to understand and debug. The above level looks like this inside my game object:
[["#", "#", "#", "#", "#", "#", "#" ]["#", "@", " ", " ", "$", ".", "#" ]["#", "#", "#", "#", "#", "#", "#" ]]
To move the player around the level, direction coordinates are passed to the game object in XY notation e.g. right is [0, 1]. If the move is legal (only one box can be pushed at a time), it's applied to the internal level state. During a move, there's some thorny logic to place the correct characters because players and boxes have two states, on goal and off goal.
A history of level states is also stored to enable undo/reset functionality. This is pretty important when a player is 100 moves deep in a puzzle and hits a deadlock.
Initially, I used a puzzle set that I created myself but, during development, I fell in love with the Minicosmos set by Aymeric du Peloux — shared by the Sokoban for the Macintosh creator Scott Lindhurst, "Many of the levels come in pairs: a relatively easy level with two stones, followed by a more challenging level with the same layout and an extra stone. This is a nice way of providing hints."
Finally, I built a quick UI with Next.js and a Sokoban skin from Boxxle (倉庫番) — play it at https://sokobanz.vercel.app.
Solving
Like chess engines, Sokoban solvers must be smart or they will never finish running within our lifetimes. Solvers must overcome a large branching factor (potentially 3-4x greater than chess) and a deep search tree (the hardest human-solveable levels require thousands of moves). In Sokoban: Improving the Search with Relevance Cuts, Junghanns and Schaffer state that:
The search space complexity for Sokoban is O(10^98) for problems restricted to a 20x20 area.
Sokoban problems require "sequential" solutions. Many of the subgoals interact, making it difficult to divide the problem into independent subgoals.
They also highlight the fact that, Sokoban problems are a directed graph where parts of the graph do not contain solutions (meaning: deadlocks — states with no solution). Pattern databases are the state of the art heuristic for detecting deadlocks.
I'll describe my solver by stepping through its creation, starting with a brute force breadth-first search. Take the following level:
########@ $.########
By generating legal moves, we can explore different branches until all the boxes (in this case, a single box) are on all of the goals. There is a single legal move to begin r. Traveling down our first branch, we have a new level state:
######## @ $.########
Now there are two legal moves: l and r. These branches are queued, and then on the third iteration we check rlr and rrl before checking and confirming a solution of rrR.
Perhaps you noticed the flaw here. We're repeating work by checking the same level state twice when we end up backtracking to a place we've been before. We can store the already-seen level states in a transposition table and avoid creating branches that perform duplicate work.
By using a transposition table (literally just stringifying the level and adding it to a set) we reduce the work required for the below two-box level by 970%!
########@ $. ## $ .########
Another improvement we can add is move ordering. When we queue up branches, we can use naïve heuristics to sort them from most-to-least promising — and then check the most promising branches first. This reduces the search tree in the final iteration.
Here are two move ordering ideas I added to my solver:
- Prioritize moves that push boxes onto goals.
- Then sort by the total Manhattan distance of boxes to goals (without taking blocking objects into account) — a lower total implies we're heading towards a more likely solution. Using A* Search here is better but I decided to cut that corner.
These reduce the work required for the two-box level by an additional 6%. See the heavily commented solver.ts file for more information on my searching and heuristic algorithms.
Without optimizing for runtime or space, my memory-hungry solver is much faster than me at solving the 40 levels I've bundled into the game.
In the face of this newly created robot adversary, I'm working on creating a level that takes an equal length of time for us (myself and my solver) to come up with a solution.