In JavaScript, you can create random numbers using Math.random(). But what if we wanted to create our own random values in the browser without this function?
The ECMAScript Language Specification defines the requirements of Math.random():
Returns a Number value with positive sign, greater than or equal to 0 but less than 1, chosen randomly or pseudo randomly with approximately uniform distribution over that range, using an implementation-dependent algorithm or strategy. This function takes no arguments.
Each Math.random function created for distinct realms must produce a distinct sequence of values from successive calls.
Number Generation
Here's an example of a number generator. It uses a closure to maintain internal state and creates a sequence of numbers based off an initial seed value. Here the seed is fixed and is always initialized to 0.
Math.random = (function () {let seed = 0return function () {seed += 1return seed}})()// We can iterate through the sequenceMath.random() // 1Math.random() // 2Math.random() // 3
A pseudorandom number generator (PRNG) works in a similar manner. A PRNG maintains an internal state and applies math to that state every time a new random number is requested. The seed can be manual or automatic. In the Go programming language, you must seed math/rand yourself. In the browser, Math.random requests random data under the hood from the operating system (OS) to use as a seed.
PRNGs are deterministic. The same seed will always produce the same sequence of numbers. Often, a deterministic outcome is preferred. For example, to generate the same random events on all clients without them having to talk over a network. Or for reproducible performance benchmarks.
A hash function can be used to create a PRNG. In spinning-balls, one of Chrome's benchmarks, we can see an example of this:
// v8/benchmarks/spinning-balls/v.js// To make the benchmark results predictable, we replace Math.random// with a 100% deterministic alternative.Math.random = (function () {var seed = 49734321return function () {// Robert Jenkins' 32 bit integer hash function.seed = seed & 0xffffffffseed = (seed + 0x7ed55d16 + (seed << 12)) & 0xffffffffseed = (seed ^ 0xc761c23c ^ (seed >>> 19)) & 0xffffffffseed = (seed + 0x165667b1 + (seed << 5)) & 0xffffffffseed = ((seed + 0xd3a2646c) ^ (seed << 9)) & 0xffffffffseed = (seed + 0xfd7046c5 + (seed << 3)) & 0xffffffffseed = (seed ^ 0xb55a4f09 ^ (seed >>> 16)) & 0xffffffffreturn (seed & 0xfffffff) / 0x10000000}})()
Like our number generator, it alters its internal state while calculating the next random number. This state-change allows the next call to produce a different number.
More on Pseudorandom Number Generators
One of the oldest and most well known types of PRNG is the linear congruential generator (LCG). Which, despite its somewhat scary name, does not require many lines of code.
@bryc provides an example and a warning:
Commonly called a Linear congruential generator (LCG), but in this case, more correctly called a Multiplicative congruential generator (MCG) or Lehmer RNG. It has a state and period of 2^31-1. It's blazingly fast in JavaScript (likely the fastest), but its quality is quite poor.
function LCG(a) {return function () {a = Math.imul(48271, a) | 0 % 2147483647return (a & 2147483647) / 2147483648}}
(This is the first time I've come across Math.imul() — which provides C-like 32-bit multiplication of the two parameters.)
What does @bryc's comment, "its quality is quite poor" mean in this context? Well, given certain even seeds, this algorithm has a pattern when the final step (the division) is removed.
// https://gist.github.com/blixt/f17b47c62508be59987b#gistcomment-2792771// @bryc:// "Looking at the output without the division, and in hexadecimal, the// first bits are always the same. This shows a clear pattern in the// first 8 bits of the output: 1000 000, and it happens each time,// infinitely. This is mostly caused by using an even seed."const LCG = (s) => (_) => (s = Math.imul(48271, s) >>> 0)const nxt = LCG(3816034944)for (let i = 0; i < 9; i++) {console.log(nxt().toString(16))}/* Outputs:4b6c5580 <-- notice the last two digitsb04dc280 <--9645a58016717280d974f5805c9f22809a3a4580f196d280b5d59580 */
There are many ways to test the quality of randomness. Some of the methodology and results of these tests can be understood by a layperson. One of the Diehard battery of tests plays 200000 games of craps and looks at the distribution of wins and the number of throws each game.
There's also a test for LCGs called the spectral test which plots the sequence in two or more dimensions. In the example below, we can see the hyperplanes that the spectral test measures for.
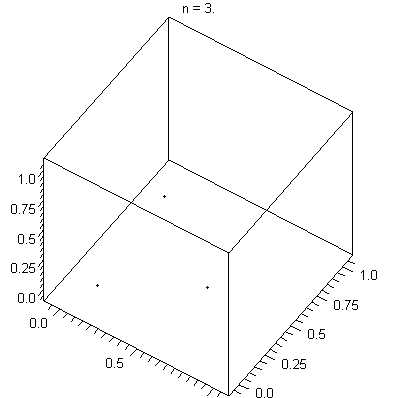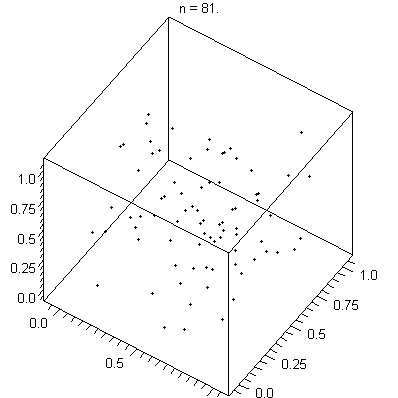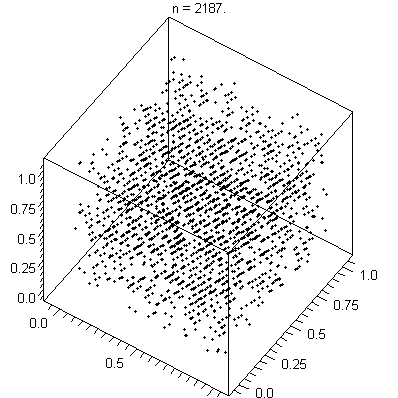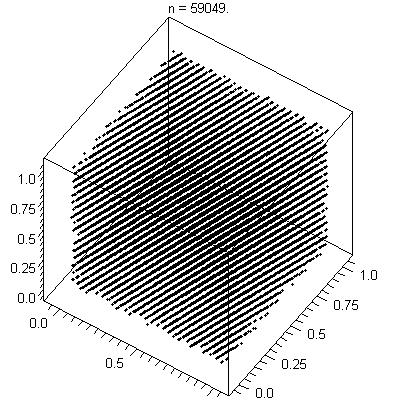
A PRNG eventually repeats its sequence. In this context, the period is the length of steps until the cycle repeats. Simpler PRNGs such as Mulberry32 have a period as low as ~4 billion whereas the Mersenne Twister has a period of 2^19,937 - 1. In 2015, the V8 team said that their implementation of Math.random() uses an algorithm called xorshift128+ which has a period of 2^128 - 1. Its introduction can been seen in this diff.
If a PRNG eventually repeats itself, you might wonder why we call it repeatedly. Why not use the first number and then reset the internal state with a new seed? The problem with this is that the seed needs to originate from somewhere. If we continue to ask the OS for more random data there is a chance that the call may block (as the OS waits for more randomness to be generated) and our program will stall.
Entropy Required
So you've settled on a PRNG and replaced window.Math.random. You've shipped it to your users and, at first, everyone seems to be happy.
But wait! You forgot about the seed. And now your users are complaining about the sequence of random numbers they get. It's the same every time their customers' page loads. All of their software is predictable. As a result, the web games they built are easy to beat.
Huzaifa Sidhpurwala reminds us:
Entropy is the measurement of uncertainty or disorder in a system. Good entropy comes from the surrounding environment which is unpredictable and chaotic.
When required, the generation of securely random numbers in the browser is performed by Crypto.getRandomValues() from the Web Cryptography API. Which is seeded by "a platform-specific random number function, the Unix /dev/urandom device, or other source of random or pseudorandom data."
The Linux source suggests where this pseudorandom data can come from:
Sources of randomness from the environment include inter-keyboard timings, inter-interrupt timings from some interrupts, and other events which are both (a) non-deterministic and (b) hard for an outside observer to measure.
There are also hardware devices that use quantum mechanical physical randomness.
You can find many prominent examples of random number generator attacks which occurred because the wrong type (or not enough) entropy was used. Cloudflare famously uses lava lamps as an entropy source. Since we are not attempting to create a secure algorithm, predictable sources of entropy like time are fine.
We can use Date.now() our seed state. This means that we will get a different random sequence for every millisecond. We could also use performance.now() which returns the length of time since the time origin.
Other possible ways of getting entropy in the browser:
crypto.getRandomValues,cryptokey generation, or similar (feels like cheating)- Mouse/touch events, ambient light events, mic/webcam noise (hard to use on page load)
- Geolocation API, Bluetooth API, or similar (need permission, doesn't work on page load)
- WebGL/video performance shenanigans
- Most APIs listed here
Here's our slower (because it's not native code) and unstable (because I haven't tested it) replacement for Math.random(). Also note that PRNGs have requirements for the seed state (e.g. prime numbers, 128-bit). Our algorithm doesn't comply with the seed recommendations for the Xoshiro family.
// https://github.com/bryc/code/blob/master/jshash/PRNGs.md// xoshiro128+ (128-bit state generator in 32-bit)Math.random = (function xoshiro128p() {// Using the same value for each seed is _screamingly_ wrong// but this is 'good enough' for a toy function.let a = Date.now(),b = Date.now(),c = Date.now(),d = Date.now()return function () {let t = b << 9,r = a + dc = c ^ ad = d ^ bb = b ^ ca = a ^ dc = c ^ td = (d << 11) | (d >>> 21)return (r >>> 0) / 4294967296}})()Math.random() // 0.5351827056147158Math.random() // 0.2675913528073579
So, Mission Accomplished?
Sadly it's impossible to create a fully ECMAScript compliant replacement for Math.random() since the specification requires "distinct realms [to] produce a distinct sequence of values from successive calls." A realm roughly means a different global environment (e.g. a different window, or a different WebWorker). Our version cannot reach outside its realm thus cannot make this guarantee.
However, there have been proposals for a Realms API. It's not inconceivable that such an API would provide access to something like an incrementing realm id. This would give our algorithm the loophole it needs — access to Realm-unique entropy!
Thanks to JN~commonswiki for the 3D GIF of the spectral test.