Christopher Langton defines artificial life as the synthetic approach to biology: rather than take living things apart, artificial life attempts to put living things together. Langton's ant attempts to capture emergent collective behaviors observed in insect colonies.
It's a cellular automaton with a set of very simple rules. The ant's universe is a grid of black and white cells that wraps around at the edges.
- The ant steps forwards in the direction it's facing
- If the new cell is white, it turns it black and rotates 90 degrees clockwise
- If the new cell is black, it turns it white and rotates 90 degrees anti-clockwise
As the ant starts to wander, these rules create messy, complex behavior. After around 10,000 steps, the ant creates a highway. Without grid edges, the highway is infinite in length.

The above figure is from The Computational Beauty of Nature (a book I highly recommend). There aren't any code examples in the book so I made my own to play around with these ants.
Let's start with a single ant. We need a grid that starts entirely white. We'll use R and L to define white and black because the ant turns right on white and left on black.
const grid = [['r', 'r', 'r', 'r', 'r'],['r', 'r', 'r', 'r', 'r'],['r', 'r', 'r', 'r', 'r'],['r', 'r', 'r', 'r', 'r'],['r', 'r', 'r', 'r', 'r'],] // [x][y]
An ant has an (x, y) position and a direction. A single ant traditionally starts in the center.
// x, y, directionconst ant = [2, 2, 'u']
Our step function moves the simulation onwards by applying the three rules.
function step() {if (ant[2] === 'u') {// Step forwardsant[1]++}// (.. other direction branches)if (grid[ant[0]][ant[1]] === 'r') {// Rotate ant rightant[2] = 'r'// Flip the cell's colorgrid[ant[0]][ant[1]] = 'l'}// (.. if 'l' branch)}
The grid now looks like this:
[['r', 'r', 'r', 'r', 'r'],// a single black cell// ↓ at the ant's location['r', 'r', 'l', 'r', 'r'],['r', 'r', 'r', 'r', 'r'],['r', 'r', 'r', 'r', 'r'],['r', 'r', 'r', 'r', 'r'],]
To render this in, say, a HTML canvas element, we can loop the grid and draw one-pixel-sized rectangles.
function render() {const ctx = canvas.getContext('2d')grid.forEach(x => {grid[x].forEach(y => {let color;if (grid[x][y] === 'r') {color = 'white'} else {color = 'black'}ctx.fillStyle = colorctx.fillRect(x, y, 1, 1);})})// draw before the browser's next repaint// usually 60 times per secondrequestAnimationFrame(render)}
In practice, this render function is too inefficient to be smooth at 60fps. It does extra, unnecessary work by drawing the same pixel on top of itself. One optimization is to only draw pixels when they change (left as an exercise for the reader).
Collective Self-Organization
In this six minute presentation, Chris Langton experiments with multiple ants, and pre-existing grid configurations, to give rise to what he calls collective self-organization.
Like two ants creating an endlessly expanding spiral.

Or red and blue ants (which rotate in opposite directions) that walk without leaving a trail.
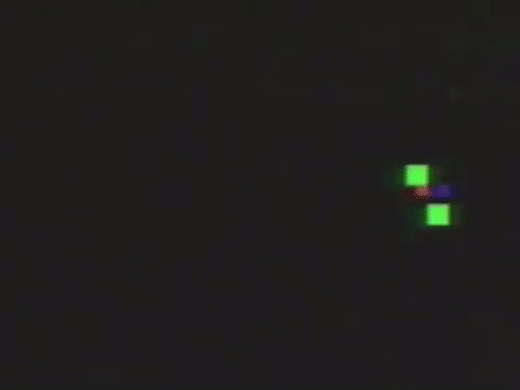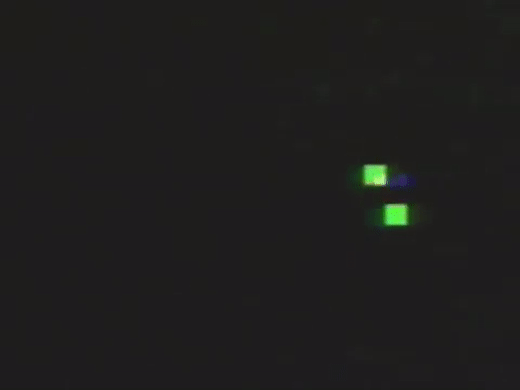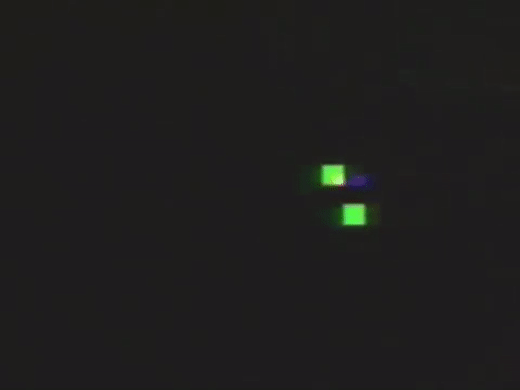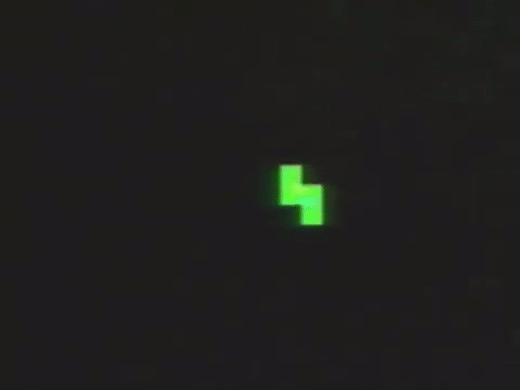
All the way up to a lively ant colony.

Multiple Colors
Langton's ant can be extended to use multiple colors. Instead of binary cells that flip from R to L (white to black) and back again, cells step through a list of turn directions (e.g. RRLRR) in a cyclic fashion.
I created a playground for this multi-color extension to Langton's ant at 🐜.vercel.app (the ant emoji is turned into punycode and looks like this: xn--ko8h.vercel.app in most browsers).
Below, a screenshot of my playground renders the progression of RRLRR — which creates an ever-expanding square.
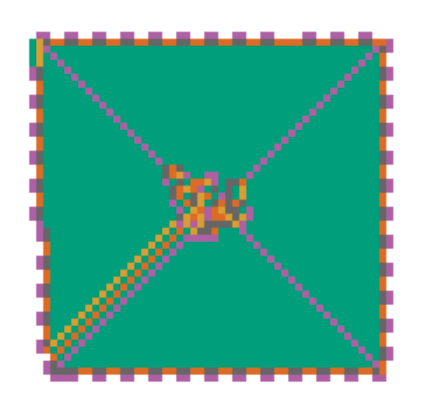
In our previous code examples, we defined a grid with 'r' or 'l' in each cell but now we need to handle additional states as the cell cycles through the list of turn directions.
We can change each cell to be an index into the list of turn directions.
const rules = ['r', 'r', 'l', 'r', 'r']// After the first simulation step with an upwards facing ant at (2, 2)const grid = [[0, 0, 0, 0, 0],[0, 0, 1, 0, 0],[0, 0, 0, 0, 0],[0, 0, 0, 0, 0],[0, 0, 0, 0, 0],]
When an ant visits a cell, it looks up the turn direction from rules, increments the index (or sets it to zero as it wraps around).
In order to support multiple ants, we can keep an ant array — and then in the step function, we can loop the array and apply the rules to each ant in turn, mutating the grid as we go.
On Prototyping
If I can build something in a few hours, I will do it without checking to see if someone has done so before because looking at other people's completed work hurts my enthusiasm to explore and learn.
The source code for my virtual ant playground consists of a single index.html file, hand-crafted over a few hours. After I pushed my code and rested, I found a far more polished and configurable version at langtonant.com.
I often write small simulations of artificial life and watch the computer pretend to be nature. Two other articles on this blog touch on artificial life — Boids, and Conway's Game of Life. It's fun when things seem alive and I enjoy the disconnect between a few neat lines of code and the beautiful chaos it spawns.
I'll leave you with a quote about this chaos from The Computational Beauty of Nature.
Ian Stewart (1994) has made an interesting observation regarding our lack of knowledge about the long-term behavior of some of these virtual ants . To paraphrase, for any of these ants we know their Theory of Everything, in that all of the "physical" laws that govern the ant's universe are simple and known to us. We also know the initial configuration of the ant's universe. Yet we are helpless to answer a simple question: Does the ant ever build a highway? Putting this all in perspective, if physicists ever uncover a Theory of Everything for our universe, and even if we deduce the initial state of the universe, we may still be helpless to deduce the long-term behavior of our own universe. Thus, as Stewart has said, the Theory of Everything in this case predicts everything but explains nothing.